Геометрическое решение

« Я называю геометрию
самым прекрасным занятием в мире,
но все же только занятием,
и я часто говорю,
что она хороша для пробы сил,
но не для того, чтобы вкладывать в нее все силы...»
(П.Ферма)

Геометрическое решение.

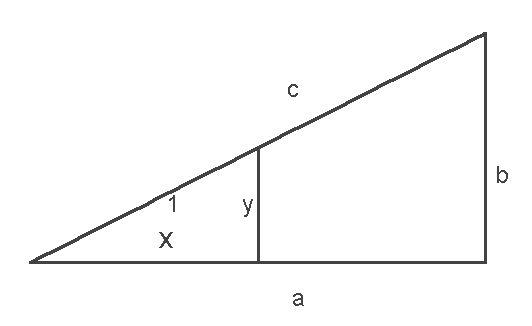
Но уравнение, которое рассматривает Ферма - xⁿ + yⁿ = zⁿ имеет три неизвестных переменных параметра, что не удобно для отображения его в двухмерной системе координат с перпендикулярными осями ХY. И здесь ему помогают великие математики прошлого. У Диофанта на этот счёт есть простое и интересное решение: в уравнение отношения сторон прямоугольного треугольника: a² + b² = c² он путём деления левой и правой его части на с, получает :

(a/с)² + (b/c)² = 1.

Если теперь принять a/c = х , а b/c = у , то получим :

x² + y² = 1 , (6)

В подобном преобразовании вместо уравнения с тремя неизвестными получаем уравнение с двумя неизвестными x и у. Эти неизвестные переменные связаны между собой функциональной зависимостью, а потому могут быть легко отражены в прямоугольной системе координат, что общем-то и требовалось для Ферма.

( Правда, вместо целых чисел а и b мы имеем дробные x и y, но в данном случае это не имеет значения, т.к. рациональные дроби всегда можно перевести в целые числа, приведя их к общему знаменателю.)

Геометрически это преобразование выглядит как пропорциональное деление сторон прямоугольного треугольника a, b, c на значение его гипотенузы c, получая в результате меньший треугольник, пропорциональный исходному, со сторонами (x; y; 1).

Рис2.а

( Такие действия чем-то напоминают "метод спуска", который Ферма применяет при решении различных задач, только в геометрическом виде.

Важно, что эти действия мы можем произвести с любым прямоугольным треугольником. Тогда получаем бесконечное число прямоугольных треугольников с различными значениями катетов, но с одинаковым значением гипотенузы, равным единичному отрезку.)

Теперь, когда Ферма обладает необходимым общим уравнением (6) и новым координатным методом ничего другого не остаётся, как построить по точкам на прямоугольной координатной плоскости изображение окружности единичного радиуса.

До середины 17 века математики настороженно относились к отрицательным числам и, хотя в 1629 году французский математик Жирар (не Декарт!) дал общеизвестный способ изображения отрицательных чисел на числовой оси, для геометрических построений чаще использовались положительные значения осей координат. Но в данном случае отрицательные числа и не нужны. Поэтому возьмём для простоты только первую четверть прямоугольной системы координат ХОY,- и её будет вполне достаточно, чтобы вместить в себя все возможные прямоугольные треугольники c единичной гипотенузой, построенные из начала координат О таким образом, что их катеты соответствуют значениям на осях координат. Геометрическое место точек уравнения (6) - это 1/4 окружности с радиусом равным единице. (Рис.3)

Далее Ферма подошёл к своему главному вопросу - что произойдет, если построить прямоугольный треугольник, стороны которого отрезки, равные числам в какой-либо степени m > 1.

Предположим, что такой прямоугольный треугольник со сторонами a^m ; b^m; c^m и m>1 - существует, а значит должен подчиняться и правилам пропорциональности.

Тогда, как и делалось ранее, геометрически поделив стороны треугольника на значение c^m (т.е. на значение гипотенузы), получим прямоугольный треугольник с катетами x^m и y^m и гипотенузой равной единице.

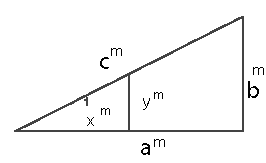
Рис.2б

Соотношение сторон в таком прямоугольном треугольнике по теореме Пифагора будет:

[(a/с)^m]² + [(b/c)^m ]² = 1

или, приняв:

a/c = x , и b/c = у

(х^m)² + (y^m)² = 1 . (7)

или, приняв 2m = n :

xⁿ + yⁿ= 1 , (где n > 2) . (8)

Ферма уже точно знает, что все прямоугольные треугольники, единичной гипотенузы, описывается окружностью единичного радиуса. Среди них должен находится и "наш" треугольник, со сторонами x^m, y^m, 1 в степени m>1 (ведь нами принято, что он - прямоугольный). Для дальнейших построений остаётся только получить точки координат из уравнения (8) и построить кривую (Рис.3) . Данная кривая, назовём её кривой F_n , является геометрическим местом точек M_i - вершин всех прямоугольных треугольников, стороны которых имеют соотношение сторон (8).

( Конечно для построений вначале брались значения n = 3 или n = 4):

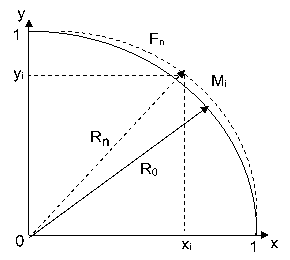
Рис.3

Но полученная кривая не совпадает с линией окружности единичного радиуса - кривая F_n имеет переменный "радиус" явно больший радиуса окружности. Этого не может быть! Ведь мы вначале брали прямоугольный треугольник (a^m , b^m, c^m), затем методом пропорционального деления его сторон получили меньший, но подобный ему прямоугольный треугольник (x^m , y^m , 1) с единичной гипотенузой, а все такие треугольники должны "помещаются" в окружности единичного радиуса. Геометрически это невозможно - ведь все полученные из (7) и (8) треугольники имеют гипотенузу больше единицы, хотя она должна быть равна единице! Истинность метода пропорционального деления доказана с помощью аксиом. Подобное противоречие можно разрешить только одним способом - такого прямоугольного треугольника со сторонами: x^m , y^m , 1 - не существует!.

Но, т.к. треугольники (x^m , y^m , 1 ) и (a^m , b^m , c^m ) - подобные, то первоначальное утверждение, что существует прямоугольный треугольник со сторонами равными (a^m , b^m , c^m ) при любом m > 1 также ложно!

Так, как мы брали произвольный треугольник (a^m , b^m , c^m ) , то вышесказанное распространяется на все треугольники такого типа - (a_i^m , b_i^m , c_i^m ) - их нельзя построить на плоскости не нарушая закона пропорциональности.

Но такие выводы только из геометрических построений, конечно, неубедительны - они должны быть подтверждены алгебраически, причём для всех значений m>1. Новый метод даёт такую возможность.

ПРИЛОЖЕНИЕ.

"Метод спуска" Ферма изложен в его 45-м примечании к "Арифметике" Диофанта и в его письме к Каркави от 1636 г, где для доказательства того, что площадь прямоугольного треугольника не может быть равна квадрату целого числа, говорилось:

"Если бы существовал некоторый прямоугольный треугольник в целых числах, который имел бы площадь, равную квадрату, то существовал бы другой треугольник, меньший этого, который обладал бы тем же свойством. Если бы существовал второй, меньший первого, который имел бы то же свойство, то существовал бы, в силу подобного рассуждения, третий, меньший второго, который имел бы то же свойство, и, наконец, четвертый, пятый, спускаясь до бесконечности. Но если задано число, то не существует бесконечности по спуску меньших его (я все время подразумеваю целые числа). Откуда заключаю, что не существует никакого прямоугольного треугольника с квадратной площадью".

(На первый взгляд довольно странная теорема. Ведь существует, например прямоугольный треугольник со сторонами 18 и 25 и площадью 15^2 . Но в то время (1636 г) построение многостепенных отрезков ещё считалось недопустимым (25=5^5 ) и геометрические фигуры с их помощью не стоились.)

Очень часто в работах о Ферма говорится, что он оставил нам абсолютно корректное доказательство своей теоремы для n=4. Но, как видим, это замечание имеет слишком общий вид и Эйлеру потребовалось не мало труда, чтобы сделать из него пригодное для математики доказательство.
Кстати, если этот метод применить к гипотетическим прямоугольникам с целочисленными сторонами (a^m , b^m , c^m ) при m>1, то его можно вполне применить и для доказательства Великой Теоремы Ферма, что возможно Ферма и сделал. Например:

"Если бы существовал некоторый прямоугольный треугольник в целых числах, который имел бы стороны, равные степеням чисел более двух, то существовал бы другой треугольник, меньший этого, который обладал бы тем же свойством. Если бы существовал второй, меньший первого, то ..."
и далее по тексту.

Впрочем, такое доказательство математики вряд ли бы приняли, хотя оно мало чем отличается от приведённого выше.

Хостинг от uCoz